고정 헤더 영역
상세 컨텐츠
본문

파이썬에는 {} 이렇게 생긴 구조를 dict(딕셔너리)라 부릅니다.
이 딕셔너리는 해시 구조로 이루어져있는데, 덕분에
원하는 키(key)에 따른 값(value)를 바로 추출할 수 있게 설계되어 있습니다.
해시
해시는 공간을 좀 더 사용해 시간을 축소시키며 (공간와 시간을 맞바꾼 기법)
데이터의 양이 어떻든 일반적인 경우 항상 O(1)을 기대할 수 있습니다.
해시는 특정 키(key)를 해시 함수를 통해 해시 테이블의 주소값으로 변경합니다.
이 과정을 해싱(hashing)이라고 합니다.
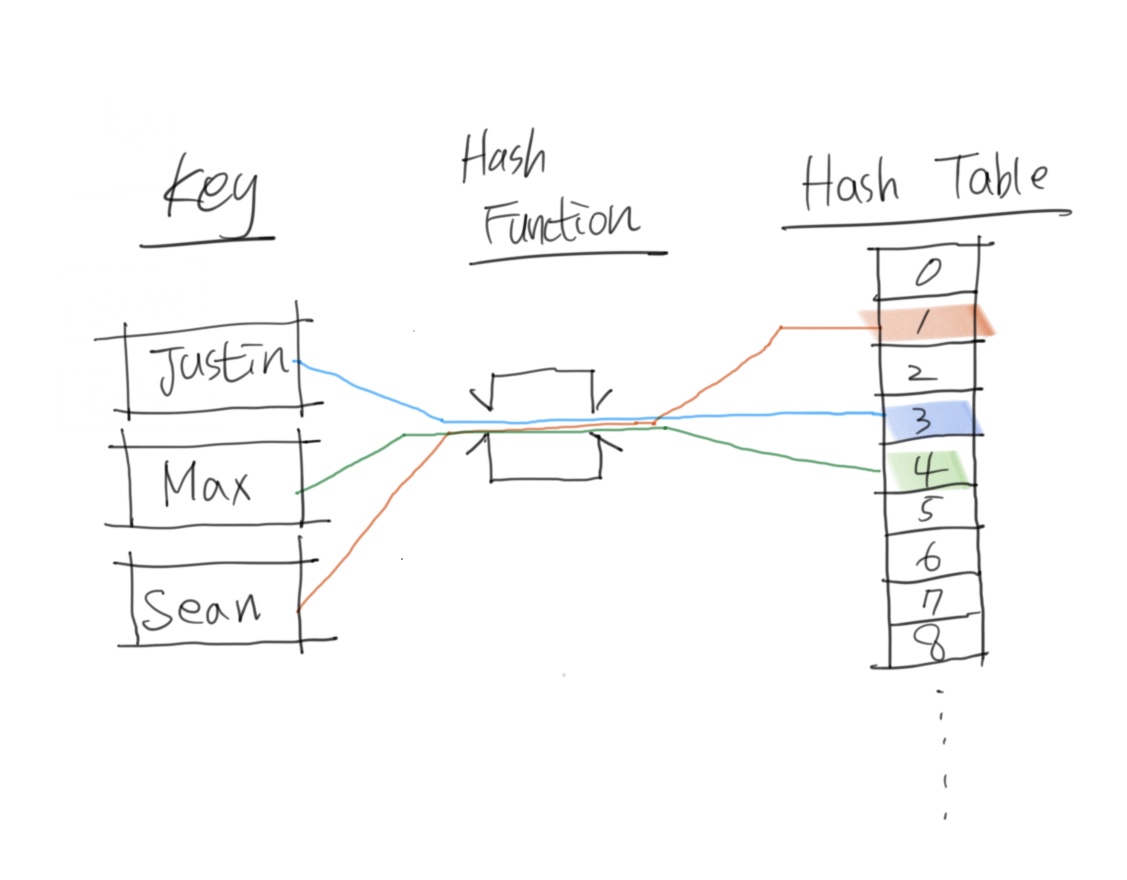

해시의 효율성
해시 함수는 해싱의 효율성을 결정하는 결정적인 요인입니다.
해시 테이블의 특정 부분만 밀도가 높아서도 안되고, (테이블 사용 효율)
연산도 빨라야 하며, 무엇보다 해시 함수 값의 충돌이 적어야 합니다.
로드 팩터(Load Factor)
위와 같은 이유로 해시 함수는 효율성이 중요하기 때문에
그 기준이 되는 척도가 있는데, 그것이 바로 로드 팩터입니다.
load factor = n / k
n : 해시 테이블에 저장된 데이터 개수
k : 해시 테이블의 총 칸(버킷) 개수
로드 팩터가 증가할 수록 해당 해시 테이블의 성능은 감소합니다.
해시 함수값이 이미 데이터가 저장된 버킷의 인덱스를 가리킬 확률이 높아지기 때문입니다.
따라서 각 언어들은 각자의 로드 팩터 기준을 정해두고,
해시 테이블이 그 기준을 넘어설 경우 해당 해시 테이블을 수정하는 과정을 거칩니다.
해시함수 값의 충돌
아무리 좋은 해시함수라 해도 해시함수 값끼리의 충돌은 일어나기 마련입니다.
만약 해시함수 값이 이미 차버린 버킷의 인덱스를 가리킨다면 다른 저장공간을 찾아야만 합니다.
이때 두 가지 방법이 있는데, 하나는 chaining 기법, 다른 하나는 linear probing 기법입니다.
chaining 기법
chaining 기법 (혹은 개별 체이닝)은 충돌이 발생하면
해당 버킷을 링크드 리스트로 연결합니다. (공간의 확장)
C++이나 자바와 같은 전통적인 언어의 경우 체이닝 기법을 많이 사용합니다.
hash_table = [0 for i in range(11)]
def save(key, value):
#임의의 해시함수
index = hash(key) % len(hash_table)
#만약 해시함수값(index)의 버킷이 이미 찼다면
if hash_table[index] != 0:
#해당 버킷에 링크드 리스트가 구현되어 있을 수도 있고,
#그 안에 해당 key값이 이미 저장되어 있을 수 있으니 찾아본다.
for data in hash_table[index]:
if data[0] == key:
data[1] = value #이미 저장되어 있다면 업데이트
return
#처음 저장하는 데이터라면 뒤에 붙여준다.
return hash_table[index].append([key, value])
#애초에 빈 버킷이었다면 2차원 리스트(링크드 리스트 흉내)로 버킷 업데이트
hash_table[index] = [[key, value]]
return#테스트 코드
import random
key_candidates = ['a','b','c','d','e','f','g','h']
for i in range(7):
save(key_candidates[i], random.randint(1,11))
print(hash_table)# 결과
[
0,
[['c', 5]],
0,
0,
[['a', 2], ['b', 4], ['e', 3]],
0,
[['f', 8]],
0,
[['d', 2]], [['g', 1]],
0
]
linear probing 기법 (오픈 어드레싱 기법)
이 방식은 충돌시 해시 테이블 안에서 빈 공간을 찾아나서는 기법입니다.
hash_table = [0 for i in range(11)]
def save(key, value):
index = hash(key) % len(hash_table)
#index(key의 주소)부터 hash_table끝까지 선형 탐색
for i in range(index, len(hash_table)):
#빈 공간이면 데이터 저장
if hash_table[i] == 0:
hash_table[i] = [key, value]
return
#빈 공간이 아니고, 데이터의 key값이 같다면, 업데이트
elif hash_table[i][0] == key:
hash_table[i][1] = value
return# 결과
[
['f', 2],
0,
['b', 7],
0,
['a', 1],
['c', 1],
['e', 3],
['g', 2],
0,
['d', 2],
0
]
linear probing 기법을 쓰면 전체 버킷 개수 이상으로 데이터를 저장할 수 없기 때문에
어느정도 해시 테이블이 채워지면 더 많은 버킷을 가진 테이블이 새로 생성됩니다. (리해싱)
또한 해시함수 값을 인덱스의 시작으로 하여 빈 공간을 찾아 나서기 때문에
해시 테이블의 특정 부분에 데이터가 몰리는 상황이 발생할 수도 있습니다.
이런 상황을 클러스터, 혹은 클러스터링이라 합니다.
따라서 linear probing 기법은 데이터가 많을 수록 효율성이 급격히 떨어집니다.
파이썬의 선택
파이썬의 경우 linear probing 기법을 우선적으로 쓰도록 설계되어 있습니다.
chaining 기법에 필요한 링크드 리스트 구현에 큰 오버헤드가 요구되기 때문입니다.
물론 linear probing도 해시 테이블의 밀도가 높아지면 오버헤드가 더 커지게 됩니다.
그래서 파이썬은 로드팩터를 낮게 잡아 이런 불상사를 미연에 방지한다고 합니다.
'소프트웨어 > 자료구조 + 알고리즘' 카테고리의 다른 글
| [정렬 알고리즘 시리즈] 버블정렬(Bubble Sort) (0) | 2022.05.07 |
|---|---|
| 프로그래머스 / 올바른 괄호 / level2 / 파이썬 (0) | 2021.12.19 |
| 백준 / DFS / 2667 : 단지번호 붙이기 / 파이썬 (0) | 2021.03.23 |
| 프로그래머스 / 크레인 인형뽑기 게임 / level 1 / 파이썬 (1) | 2021.03.21 |
| 복잡한 isPalindrome / 정규표현식 re.sub() or isalnum() / leetcode 125번 (0) | 2021.03.06 |





댓글 영역