고정 헤더 영역
상세 컨텐츠
본문

인덱싱의 필요성
데이터베이스에서 어떤 데이터를 가져오려 하는 상황을 가정해 봅시다. 이때 모든 데이터를 풀 스캔(처음부터 끝까지 쭉 탐색)으로 가져온다면 데이터를 가져오는 시간은 매우 오래 걸릴 것입니다. 특히나 데이터베이스 시스템은 디스크 기반이라 I/O 작업에서 상당한 시간을 소모합니다.
보통 디스크의 작업 속도가 얼마나 느린지를 가늠하기 위해 CPU, 메모리와 비교하곤 하는데, CPU와 메모리 모두 보통의 경우 나노세컨드 단위가 언급되는 반면 디스크는 밀리세컨드 단위가 소요되기 때문입니다.
디스크는 왜 느린가요?

데이터를 읽기 위해서는 *헤드를 움직여 데이터가 저장된 위치(*트랙)를 찾아야 합니다. 이때 소요되는 시간을 탐색 시간(seek time)이라고 합니다. 그 후 원하는 정보가 있는 *섹터가 다가올 때까지 기다리는데 이때의 시간을 회전 대기 시간(rotational latency time)이라고 합니다.
*헤드 : 상단 이미지에서 디스크 오른쪽에 있는 회색 꺾쇠의 디스크와 닿는 부분
*트랙 : 디스크(플래터)의 한 면에서 중심으로부터 같은 거리에 있는 섹터들의 집합
*섹터 : 데이터 저장/판독의 물리적 단위
따라서 데이터베이스의 I/O 처리 작업은 이렇게 물리적인 작업을 거치기 때문에 다른 자원들보다 더 오랜 시간이 소요될 수밖에 없습니다. 데이터베이스와 통신하는 API를 짜 본 사람들은 최대한 DB 히트를 줄이려는 노력을 해봤을 텐데, 그 이유가 바로 이것입니다.
B-Tree
빠른 데이터 액세스를 위해 여러 자료구조/알고리즘 논의가 있어왔고, B-Tree는 그 중 가장 대표적인 구조입니다. B-Tree는 컬럼의 값과 해당 레코드가 저장된 주소 or 자식 노드 페이지 주소를 key : value로 인덱스화합니다.
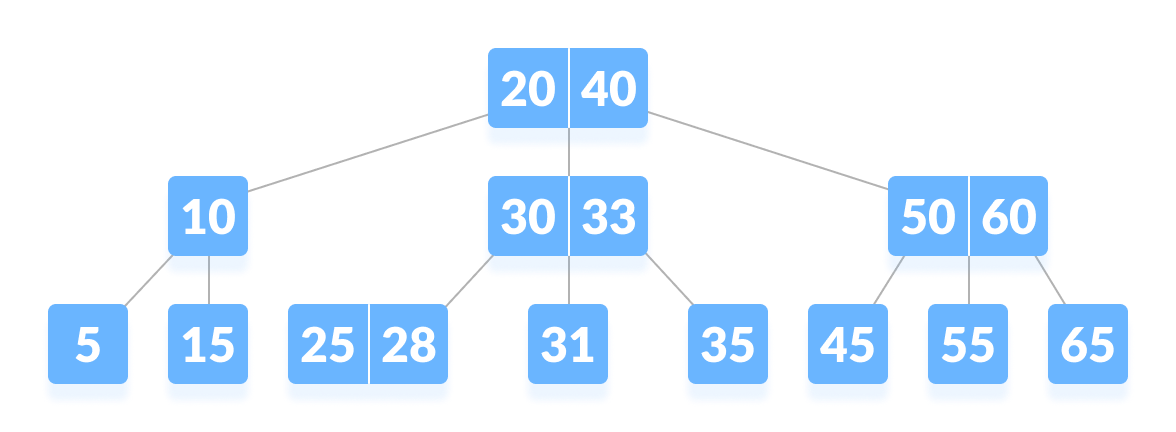
B-Tree는 binary tree(이진 트리)에서 파생된 트리 구조입니다. 이진 트리와의 차이점이 있다면, 하나의 노드는 2개 이상의 데이터를 가질 수 있다는 점, 그리고 자식 노드도 여러 개를 가질 수 있다는 점입니다. 이런 B-Tree의 특성 덕분에 트리의 높이를 낮출 수 있게 되었습니다.
또한 이진 트리와 달리 B-Tree는 균형된 트리의 모양새를 갖추고 있습니다. 보통의 경우 트리를 이용한 탐색 복잡도는 O(logN)이라고 알려졌습니다. 하지만 트리가 한쪽으로 쏠려있을 경우에는 O(n)까지 성능이 저하됩니다.
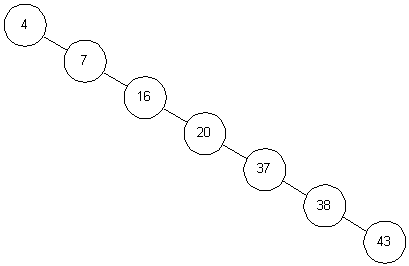
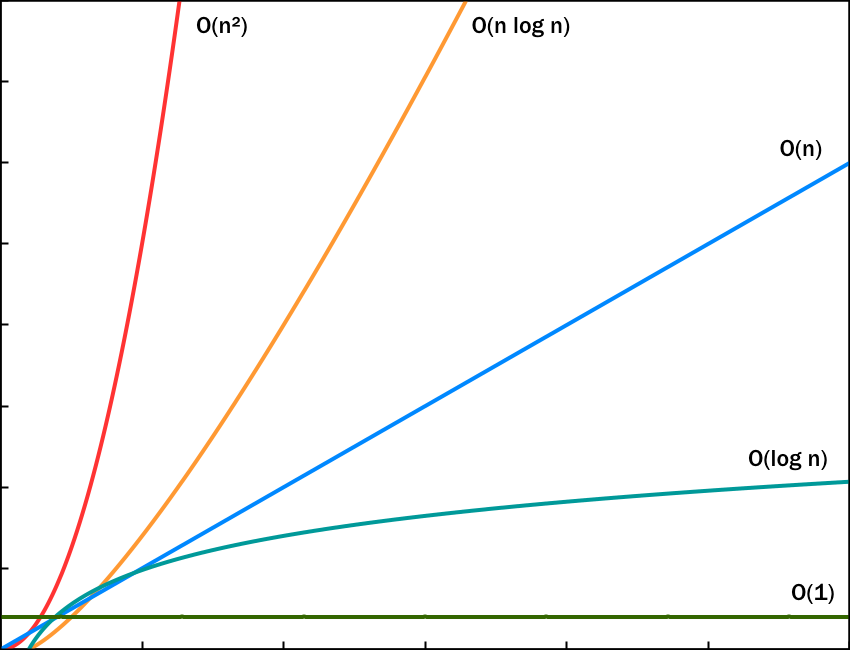
하지만 B-Tree는 INSERT, DELETE와 같은 작업이 일어나도 항상 균형을 유지하도록 되어 있습니다. B-Tree에서 앞글자 B가 binary라고 오해하기 쉽지만 사실 balanced라는 뜻이라는 걸 인지할 수 있습니다.
B-Tree 구조 규칙
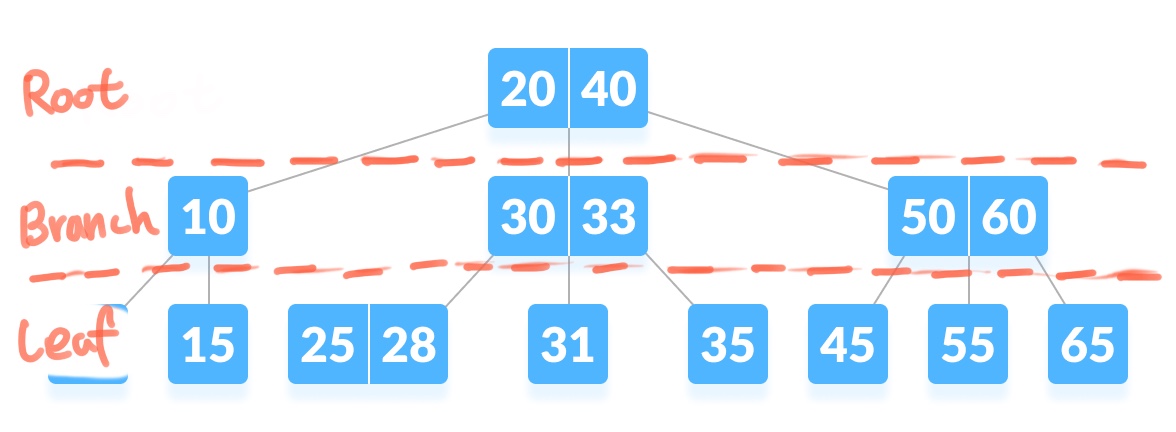
1. 최상단의 노드를 root node, 최하단의 노드를 leaf node, 그 사이 노드를 branch node라 부릅니다.
2. 노드의 데이터 수는 두 개 이상일 수 있습니다.
3. 노드의 데이터 수가 N개이면, 자식 노드 수는 N+1개여야 합니다.
(위 이미지처럼 데이터 수가 2개라면 자식 노드는 세 개씩)
4. 노드에 저장할 수 있는 데이터 수에 따라 M차 B-Tree라 부릅니다.
5. root 노드를 제외한 모든 노드는 적어도 M/2개의 데이터를 지니고 있어야 합니다.
(3차 B-Tree의 경우까지는 1개의 데이터 허용)
6. 노드 내 키(key)는 정렬(sort)된 상태여야 합니다.
(이진 트리와 동일한 규칙입니다.)
7. leaf 노드로 가는 모든 경로는 그 길이가 같아야 합니다.(트리 균형)
B+Tree
B-Tree의 한계
InnoDB(MySQL 데이터베이스 엔진)는 그렇다면 B-Tree를 사용할까요? 적어도 제가 공부한 바로는, InnoDB는 B+Tree로 인덱싱을 처리합니다.
https://dba.stackexchange.com/questions/204561/does-mysql-use-b-tree-btree-or-both
기존의 B-Tree도 한계가 있습니다. 가장 큰 단점은 바로 시퀀셜 액세스에 취약하다는 점입니다. 우리는 데이터를 가져올 때 range를 정해놓고 해당 range에 속하는 데이터를 가져오는 작업을 종종 하곤 합니다.
data = User.objects.filter(id__lte=5, id__gte=1)
아래와 같은 구조에서 위와 같은 데이터 액세스를 시도한다면, 기본적으로 B-Tree는 루트부터 하향식으로 데이터를 찾아가기 때문에 여간 복잡해지지 않을 수 없습니다. (마치 BFS를 재귀로 구현하는 느낌?) 게다가 실제 데이터는 입력 순서대로 저장되어 있지도 않기 때문에 이렇게 흩뿌려져 있는 데이터를 정렬된 형태로 보여주는 작업은 매우 복잡합니다.

추가적으로, 노드의 삭제/삽입 작업이 이루어질 때 트리의 균형을 유지해주는 작업이 필수적이기 때문에 트리의 깊이에 따라 overhead가 커집니다.
B+Tree
B+Tree는 이런 B-Tree의 단점을 보완합니다. B+Tree의 핵심은 Multilevel-indexing과 Linked-list에 있습니다.
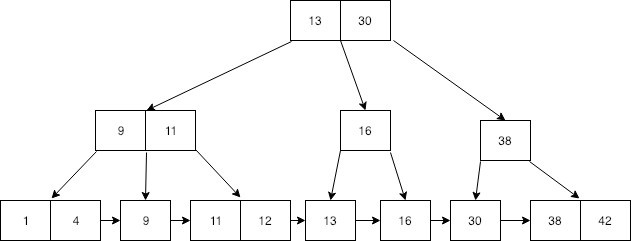
B+Tree를 간단하게 표현한 다이어그램입니다. 겉보기에는 큰 차이가 없어 보입니다. 하지만 가장 하단의 leaf node를 보면 같은 레벨의 노드들끼리 서로 linked list 형식으로 연결되어 있습니다. 시퀀셜 액세스를 효과적으로 처리하기 위해 key : value의 페이지는 leaf node에만 존재하고, 그 외 레벨의 node들은 오직 인덱싱을 위한 key를 저장하는 용도로만 사용됩니다.
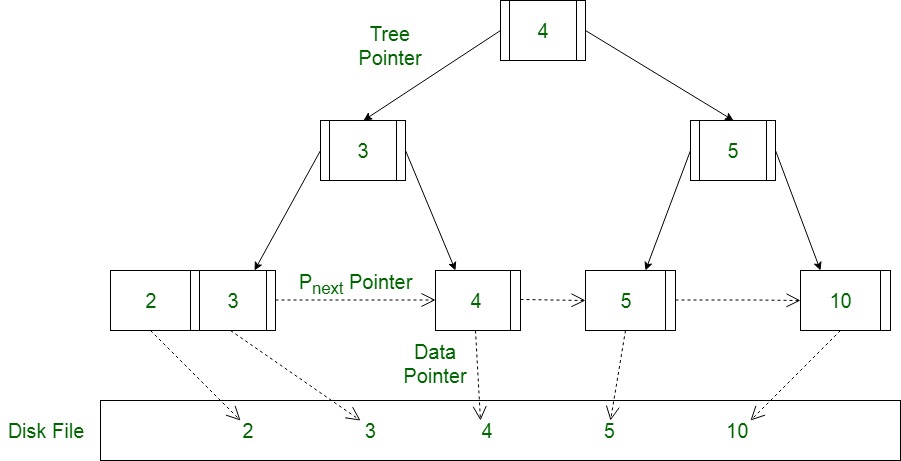
위 다이어그램은 B Tree를 너무 어렵지도 않게 잘 풀어놓은 그림이라고 생각해서 가져와 보았습니다. leaf node를 제외한 레벨의 노드들에는 더 이상 data pointer(실제 데이터가 저장된 주소 포인터)가 존재하지 않습니다. 오직 leaf node만이 실제 데이터를 가리킬 수 있기 때문에 모든 key는 leaf level에 존재해야 합니다. 따라서 B-Tree와 달리 부모 노드와 자식 노드가 같은 키를 공유할 수도 있습니다. 그리고 value를 저장하지 않아서 남는 공간에 key를 채워 넣다 보니 트리의 높이를 낮출 수 있게 되었습니다.
이런 점들이 B+Tree를 비교적 빠르고 효과적인 작업에 유리하게끔 합니다.
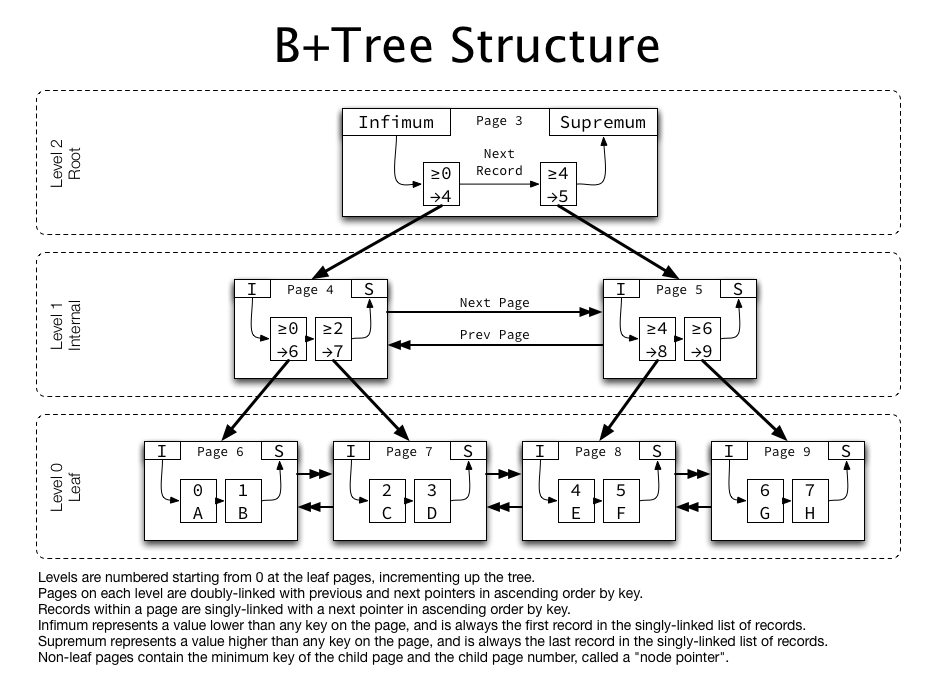
실제 InnoDB에서 쓰이는 B+Tree는 좀 더 복잡한 형상을 띄고 있습니다. leaf node들뿐 아니라 그 상위 레벨의 노드들도 링크드 리스트로 연결되어 있으며, 싱글 링크드 리스트가 아닌 더블 링크드 리스트로 보입니다.
정리
| 구분 | B-Tree | B+Tree |
| 데이터 포인터 | 모든 내부적인 노드들은 데이터 포인터를 지님 | 리프 노드에만 데이터 포인터가 존재 |
| 시퀀셜 액세스 탐색 방식 | 모든 key가 리프 노드에 존재하지 않기 때문에 모든 노드를 탐색해야 함 | 모든 key가 리프 노드에 존재하기 때문에 리프 레벨에서만 탐색하면 됨 |
| 키 중복 여부 | 모든 노드는 서로 다른 key를 지님 | 부모 노드와 자식 노드가 같은 키를 가질 수 있음 |
| 삽입/삭제 복잡도 | 비교적 복잡함 | 비교적 간단함 |
| 링크드 리스트 | 존재하지 않음 | 리프 노드는 링크드 리스트로 연결되어 있음 |
이런건 왜 알아야 할까?
https://www.quora.com/Why-and-when-do-you-need-to-rebuild-indexes-in-SQL-databases-for-performance
Why and when do you need to rebuild indexes in SQL databases for performance?
Answer (1 of 3): Thanks for A2A. The answer to your question lies in fields of definition of indexes in the popular modern RDBMS. Most of them used B+ Tree indexes (I will not touch Bitmap or other indexes, but the situation is the same of them): this is a
www.quora.com
참고
[Real MySQL] B-Tree 인덱스
인덱스는 데이터베이스 쿼리의 성능을 언급하면서 빼놓을 수 없는 부분입니다. MySQL에서 사용 가능한 인덱스의 종류 및 특성에서 각 특성의 차이는 상당히 중요하며, 물리 수준의 모델링을 할
12bme.tistory.com
https://www.programiz.com/dsa/b-plus-tree
B+ Tree
B+ Tree In this tutorial, you will learn what a B+ tree is. Also, you will find working examples of searching operation on a B+ tree in C, C++, Java and Python. A B+ tree is an advanced form of a self-balancing tree in which all the values are present in t
www.programiz.com
https://www.geeksforgeeks.org/difference-between-b-tree-and-b-tree/
Difference between B tree and B+ tree - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
https://www.aladin.co.kr/shop/wproduct.aspx?ItemId=65822861
그림으로 공부하는 오라클 구조
일본의 데이터베이스 잡지인 DB Magazine의 인기 연재물 ‘그림으로 공부하는 오라클 입문’을 재구성한 책이다. 오라클 아키텍처의 세계를 그림으로 체험함으로써 그 어떤 오라클 책보다도 쉽고
www.aladin.co.kr
'데이터베이스' 카테고리의 다른 글
| Row vs Column oriented Databases (1) | 2023.12.04 |
|---|





댓글 영역