고정 헤더 영역
상세 컨텐츠
본문 제목
플로이드의 토끼와 거북이 알고리즘(Floyd's Tortoise & Hare Algorithm) / 증명 / leetcode 287번 / 파이썬
본문

발단
어느날 나의 유튜브 알고리즘에 뜬 JOMA...
사실 예전에도 한 번 본 적 있는 영상인데
그때는 킬킬킬 웃고 넘어갔지만 이제와서 다시 보니 알고리즘의 내용이 궁금해졌습니다.
결국엔 알아보게 된 플로이드의 순환 알고리즘!
문제출처
leetcode.com/problems/find-the-duplicate-number/
Find the Duplicate Number - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
문제
- 자연수 N과 N + 1 길이를 가진 배열 nums가 주어집니다.
- nums에는 1보다 크거나 같고, N보다 작거나 같은 정수만 들어올 수 있습니다.
- nums에는 중복되어 들어오는 값이 딱 하나 있습니다. 해당 값을 찾아내세요.
제한사항
2 <= N <= 3 * 10^4
플로이드의 순환 알고리즘
이 문제는 단순한 1차원 리스트를 계산하는 문제인척 하는 그래프 문제입니다.
(정확히 말하자면 linked list)
이 문제를 풀기 위해 JOMA 센빠이는 플로이드의 알고리즘을 설명하고 있는데요,
우선 문제 내용은 제쳐두고, 플로이드의 알고리즘이 무엇인지 알아보도록 하겠습니다.
우리는 플로이드의 알고리즘을 이용해
주어진 링크드 리스트에 사이클이 있는지 확인할 수 있습니다.
아래와 같은 링크드 리스트가 있다고 가정해봅시다.
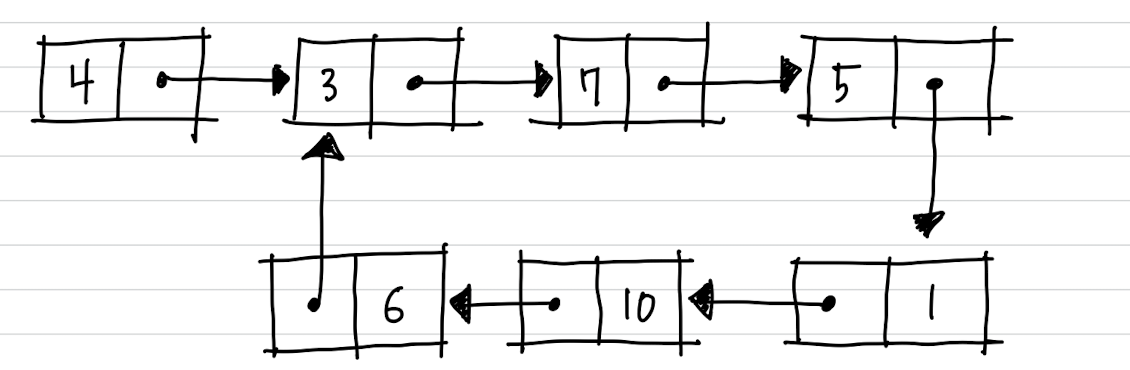
cycle 유무 찾기
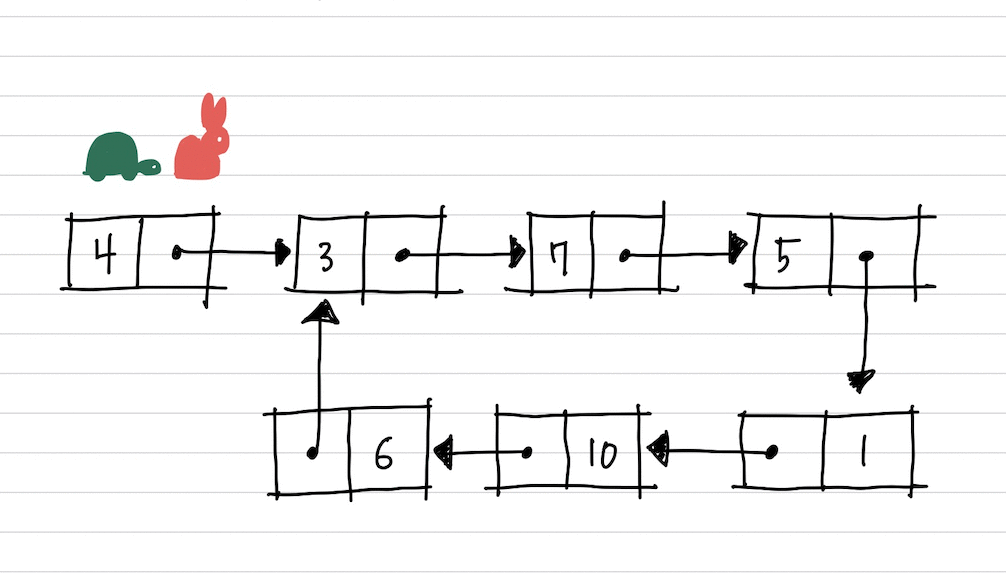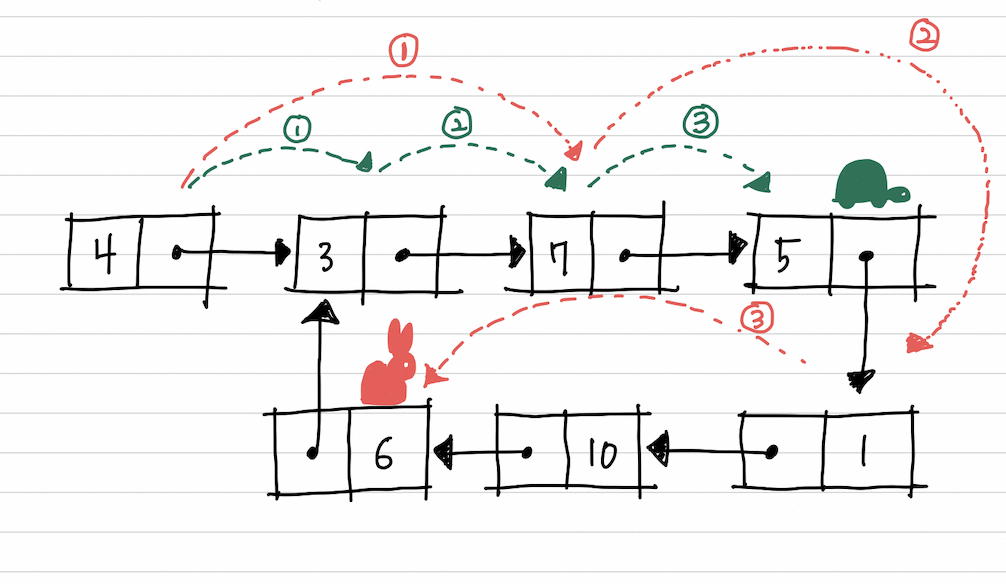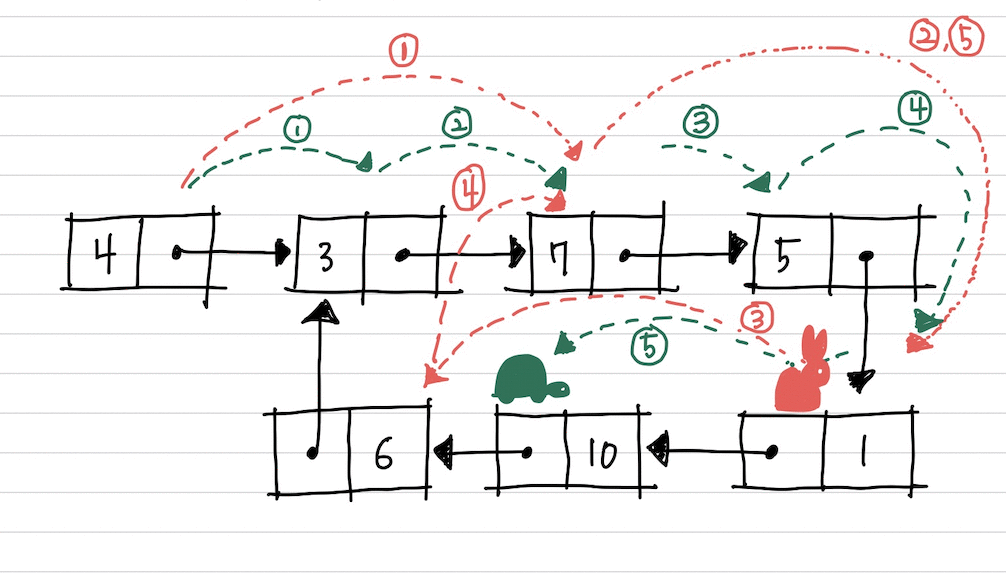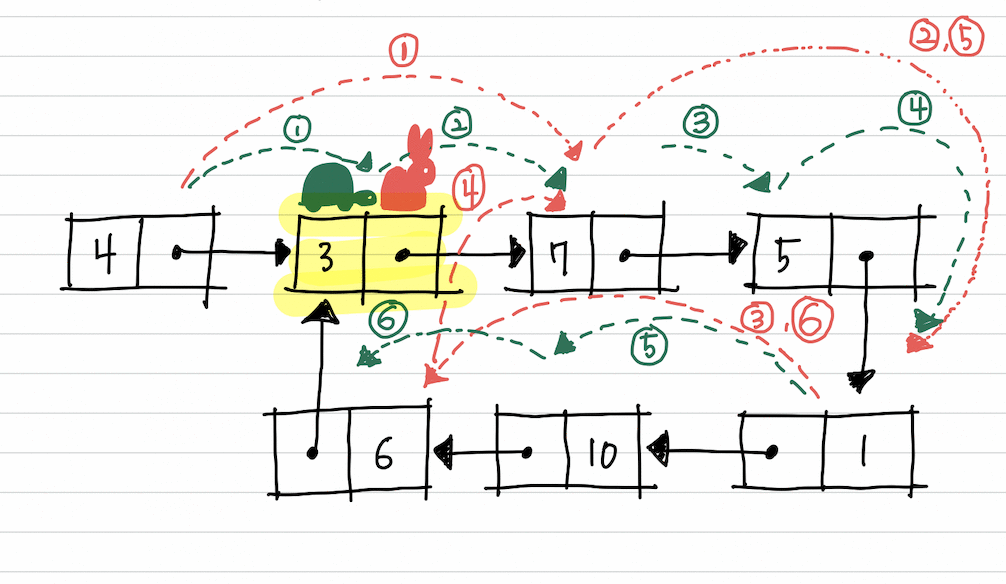
토끼와 거북이가 리스트의 root에서 출발합니다.
토끼는 빠르게 두 칸씩 이동할 수 있고,
거북이는 한 칸씩밖에 이동하지 못합니다.

만약 리스트에 사이클이 있다면,
토끼와 거북이는 언젠가 만나게 됩니다.
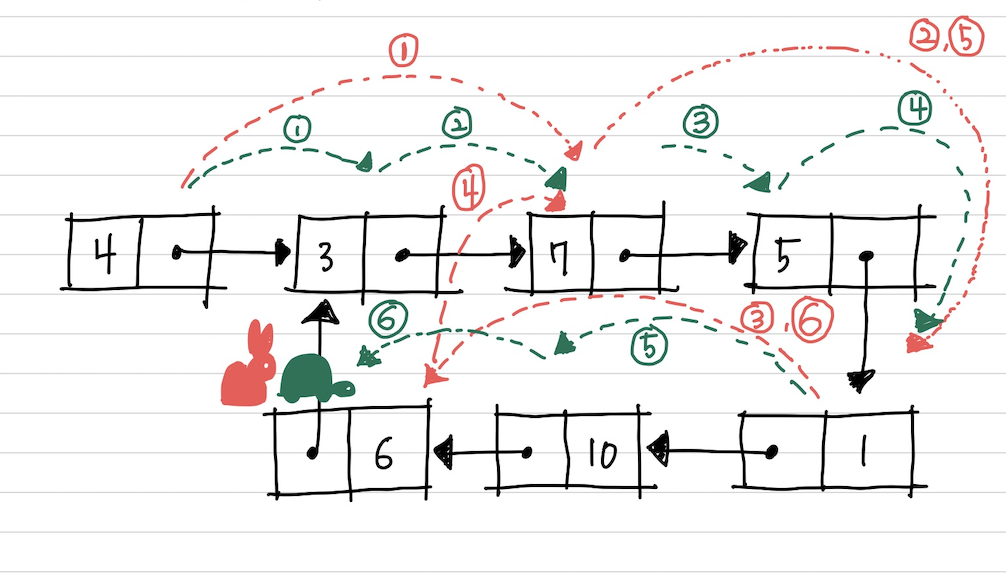
cycle 시작점 찾기
토끼와 거북이가 만났다면
거북이를 다시 시작점으로 돌려보냅니다.

이제 거북이와 토끼 모두 한 칸씩만 이동합니다.
그러던 중 둘이 처음으로 만나는 지점이 바로 순환의 시작점이 됩니다.

증명식

-
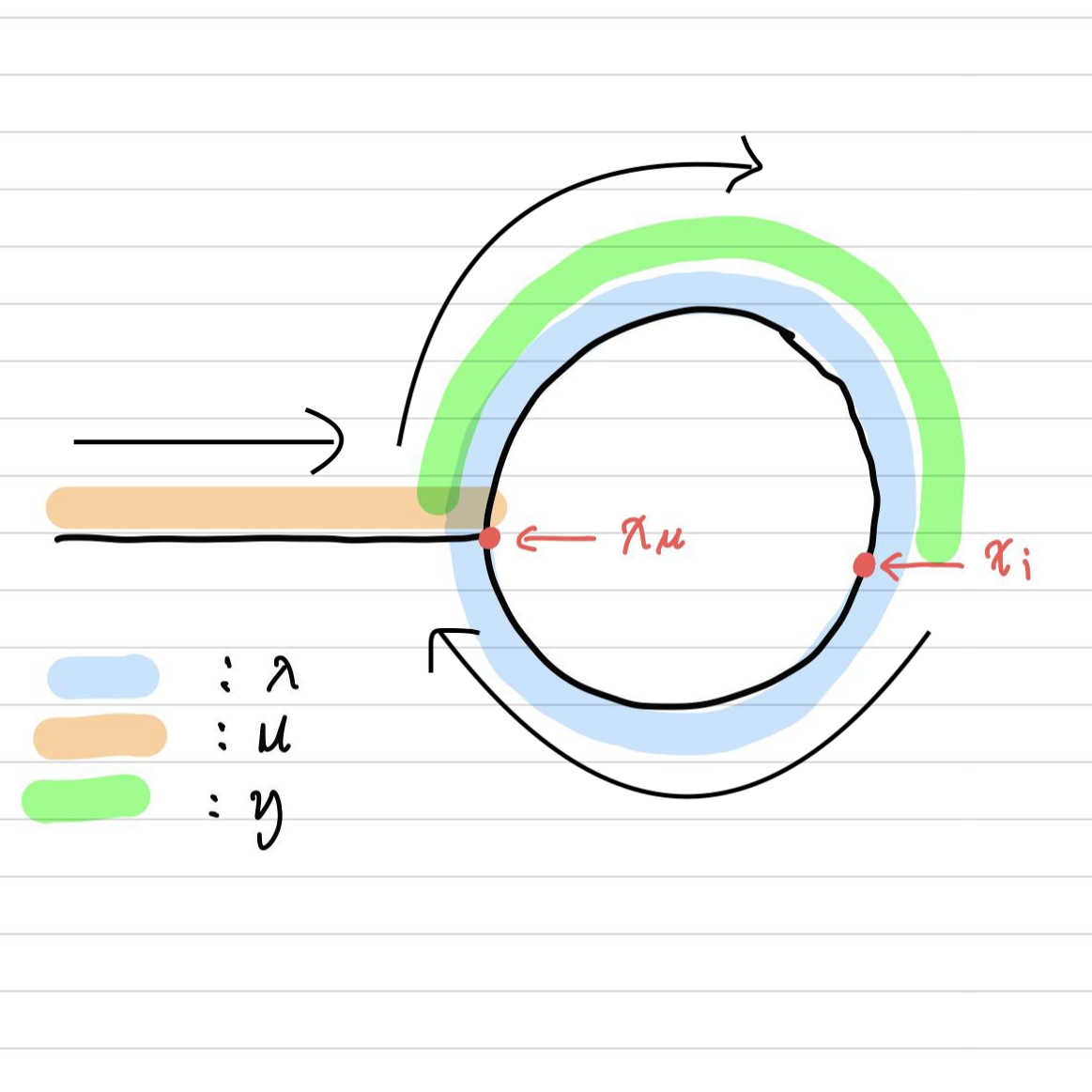
𝑖 = 토끼와 거북이가 만나기까지 거북이가 이동한 거리
-
μ = 리스트 시작점부터 사이클 시작점까지의 거리
-
λ = 사이클의 순환 길이
-
𝓍₀, 𝓍₁, 𝓍₂ ...... = 각 노드 표기
- 𝓍𝑖 = 토끼와 거북이가 만난 지점
-
m = 거북이가 사이클을 돈 횟수
-
n = 토끼가 사이클을 돈 횟수
-
y = 𝓍𝑖와 𝓍μ 사이의 거리 (즉, 사이클 시작점에서부터 토끼와 거북이가 만난 지점까지의 길이)
(1) 𝑖 = μ + (m * λ) + y
👆 거북이의 이동 거리 계산식
(2) 2𝑖 = μ + (n * λ) + y
👆 토끼의 이동 거리 계산식
토끼는 두 칸씩 이동하니까 2𝑖가 토끼의 이동 거리가 됩니다!
이제 두 식을 연립해서 풀어보면
(3) 𝑖 = (n - m)λ

(4) 𝓍(𝑗 + 𝑘 * λ) = 𝓍𝑗 (𝑗 >= μ)
사이클 내부의 임의의 정점에서 사이클 길이만큼 더해도 같은 정점이죠.
두 바퀴를 돌든, 세 바퀴를 돌든 (𝑘 * λ) 그 값은 변하지 않습니다.
여기서 𝑗에 μ를 대입합니다.
(μ = 리스트 시작점부터 사이클 시작점까지의 길이)
(즉, 사이클의 시작점)
그리고 𝑘에는 (n - m) 값을 넣습니다. (토끼와 거북이가 사이클을 돈 횟수 차이)
𝓍 (μ + λ(n-m)) = 𝓍μ
그런데 (3)에서 우리는 이미 λ(n-m)의 값이 𝑖임을 증명해냈습니다.
따라서 𝓍(μ + 𝑖) = 𝓍μ가 됩니다!!!!!!!!!!!

일차원 배열(리스트)에 적용해보기
다시 돌아와서 보니,
해당 문제는 링크드 리스트가 아니라 단순 일차원 배열에 적용해야 하는 문제네요.
그렇다면 input으로 들어온 배열을 링크드 리스트로 변환해봅시다.
JOMA 센빠이는 리스트 안에 담긴 각 value를 pointer로 치환하면 된다고 설명했습니다.
아래의 예시를 볼까요.
N = 6 # which is a given input
random_array = [1, 4, 3, 5, 6, 1, 2] # a list has N + 1 length.
각 value는 N보다 클 수 없기 때문에 반드시 array 내부의 값을 point하게 됩니다.
그리고 중복되는 값이 있다면, 해당 값이 사이클의 시작점이 됩니다.
JOMA님의 파이썬 코드
def findDuplicate(nums):
tortoise = nums[0]
hare = nums = [0]
while True:
tortoise = nums[tortoise]
hare = nums[nums[hare]]
if tortoise == hare:
break
ptr1 = nums[0]
ptr2 = tortoise
while ptr1 != ptr2:
ptr1 = nums[ptr1]
ptr2 = nums[ptr2]
return ptr1
참고
zhu45.org/posts/2017/Jun/18/the-tortoise-and-the-hare/#mjx-eqn-eqn1
The tortoise and the hare
The tortoise and the hare Date Jun 18, 2017 Tags linked-list / leetcode / algorithm Recently, I start to work on leetcode's problems. My goal is to solve two problems per day (mission possible, right?). The problems I'm looking at are 142. Linked List Cycl
zhu45.org
stackoverflow.com/questions/2936213/explain-how-finding-cycle-start-node-in-cycle-linked-list-work
Explain how finding cycle start node in cycle linked list work?
I understand that Tortoise and Hare's meeting concludes the existence of loop, but how does moving tortoise to beginning of linked list while keeping the hare at meeting place, followed by moving b...
stackoverflow.com
Floyd's Cycle detection algorithm | Determining the starting point of cycle
I am seeking help understanding Floyd's cycle detection algorithm. I have gone through the explanation on wikipedia (http://en.wikipedia.org/wiki/Cycle_detection#Tortoise_and_hare) I can see how the
cs.stackexchange.com
'소프트웨어 > 자료구조 + 알고리즘' 카테고리의 다른 글
| 복잡한 isPalindrome / 정규표현식 re.sub() or isalnum() / leetcode 125번 (0) | 2021.03.06 |
|---|---|
| 백준 / 동적 계획법(DP) / 1904 / 파이썬 (0) | 2021.03.03 |
| 프로그래머스 / 해시 / 위장 / level 2 / 파이썬 (0) | 2021.02.21 |
| 백준 / 완전탐색(brute force) / 2231 / 파이썬 (0) | 2021.02.14 |
| 프로그래머스 / 큐,스택 / 기능개발 / level 2 / 파이썬 (0) | 2021.02.06 |






댓글 영역